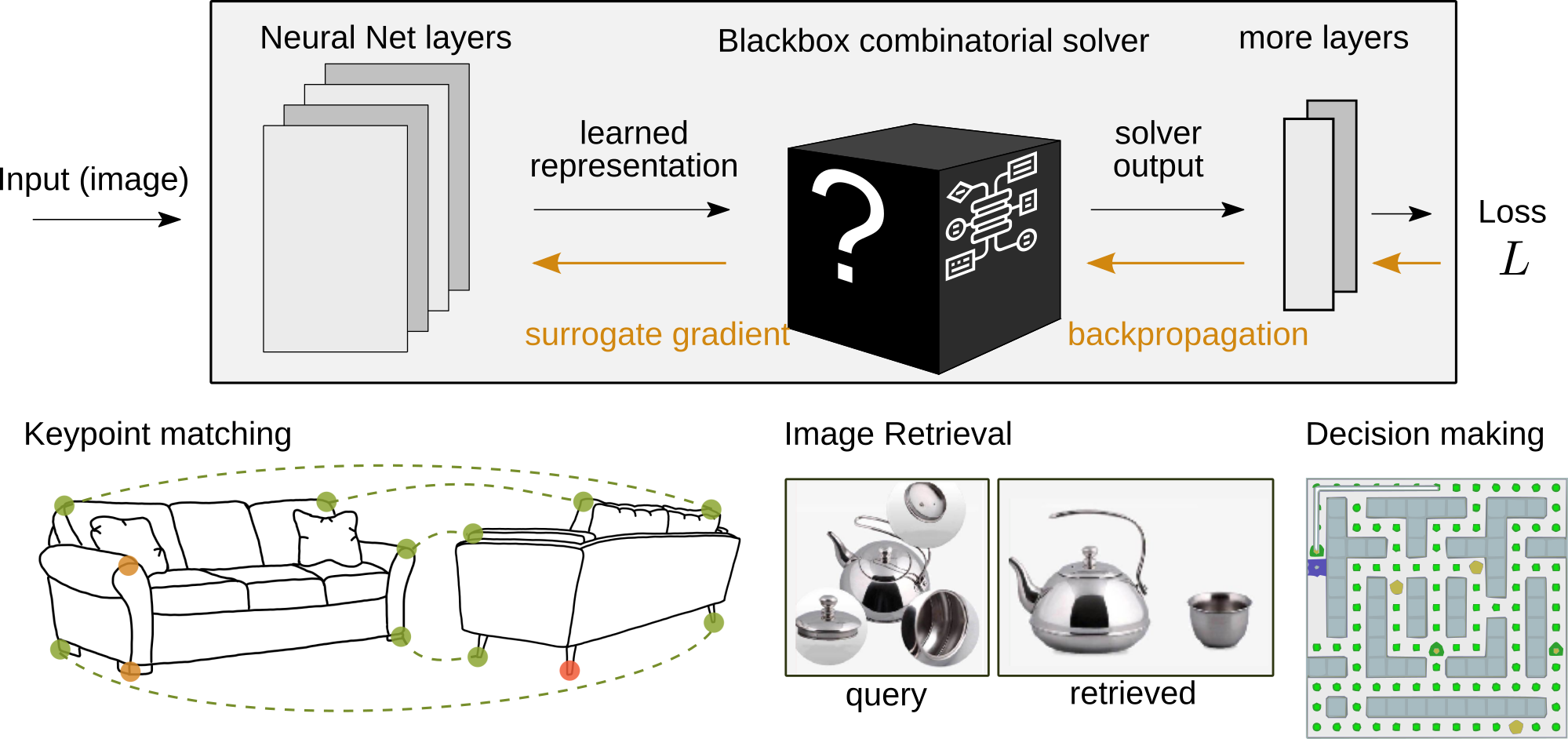
Schema depicting an architecture with an embedded solver on the top. Thanks to our surrogate gradient, training can be done as usual with stochastic gradient descent. The bottom row illustrates the applications we tackled so far: keypoint correspondence in pairs of images, directly optimizing ranked-ranked-based losses for improved image retrieval, and embedded planning for stronger generalization in reinforcement learning.
Deep learning has shown remarkable success in solving problems from high-dimensional raw input, such as image recognition or speech-to-text translation. However, deep learning is not particularly good when it comes to problems with a combinatorial nature, such as solving a puzzle, finding the shortest path or matching two sets of items. For each of these problems, computer scientists have developed highly optimized algorithms with correspondingly fast implementations in the field of combinatorial optimization. These methods require a perfect input representation and cannot be used on raw inputs as such.
In this work, we bring deep learning and combinatorial optimization together. Ideally, we would like to have the best of both worlds: having rich feature representations through deep neural networks and efficient algorithm implementations that enable combinatorial generalization. We have developed a method [ ] with which such algorithms can indeed be used as building blocks in deep neural networks. The original implementations do not need to be known or modified. Instead, it is enough to invoke them one time during the gradient computation on a modified input to obtain an informative gradient.
Equipped with our new method, called Blackbox differentiation, we tackled two real-world problems in computer vision: the keypoint correspondence problem and optimizing rank-based functions.
The keypoint correspondence problem is about finding matching pairs of points in two or more images. Our architecture embedding a strong graph-matching solver [ ], is able to outperform the state of the art in this domain on several benchmarks.
Another remarkable success of our method is that it allows computing gradients for ranking-based functions [ ] -- commonly used in, e.g., object-retrieval. Our paper was nominated for the best-paper award at CVPR.
Enhancing reinforcement learning agents with planning algorithms as part of their policy networks is another exciting application [ ].
Recently, we conceptually enhanced our method with the ability to learn the type of combinatorial algorithm that should be solved [ ]. This is achieved by learning the constraints of an integer linear program.
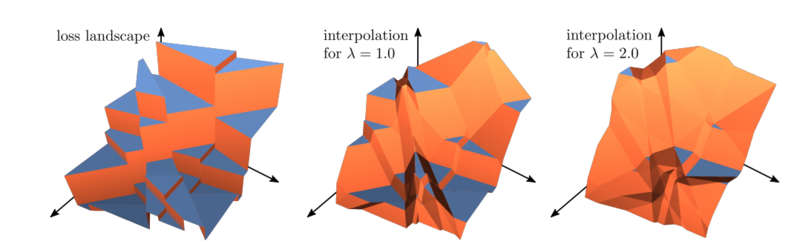
In search for practical application of the blackbox-differetiation theory, we turn to computer vision. Concretely, we show that applying blackbox-backprop to computer vision benchmarks in recall and Average Precision for retrieval and detection tasks consistently improves the underlying architectures’ performance.
The main component that enables this is the blackbox formulation of the argsort operation used for ranking making the use of blackbox-differentiation theory possible. We made a blog post describing the method, which we call RaMBO (Rank Metric Blackbox Optimization). Further information about the paper (including a short and long oral presented at CVPR 2020) can be found here.
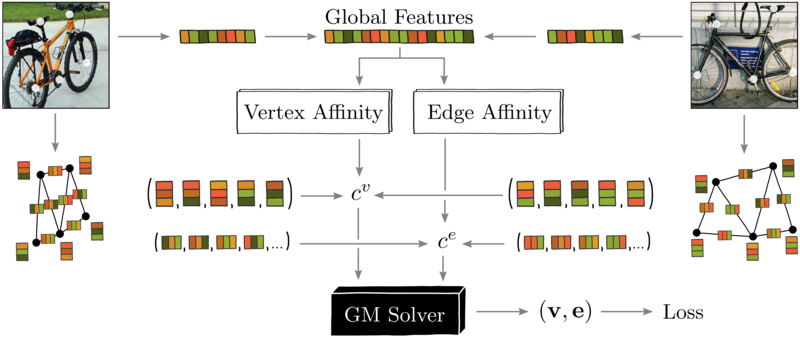
Staying in the research area of computer vision, we tackle the problem of keypoint matching. Leveraging our blackbox-backprop framework, we carefully extract keypoint descriptors using visual and geometrical information and use a state-of-the-art solver to solve a bipartite graph matching problem. The resulting end-to-end trainable architecture set the state-of-the-art on challenging keypoint matching benchmarks when it was published at ECCV 2020.
Further information about the paper can be found here.
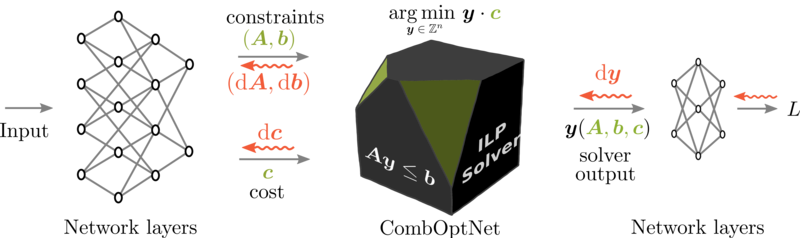
While this project is not directly using the blackbox differentiation framework, its spirit is closely linked to the idea of using combinatorial solvers in deep neural networks. This paper asks the question, whether it is possible to design an architecture that is not taylored to one specific combinatorial problem as in the blackbox differentiation framework, but instead offers universal combinatorial expressivity.
We describe `CombOptNet´, which learns the underlying combinatorial problem that governs the training data, by learning the parameters of the full specification of a general Integer Linear Program. Specifically, we show that we can solve challenging tasks such as knapsack problems from natural language description, as well as visual combinatorial graph matching, without a priori specifying the underlying combinatorial problem.
Further information about the paper can be found here.
