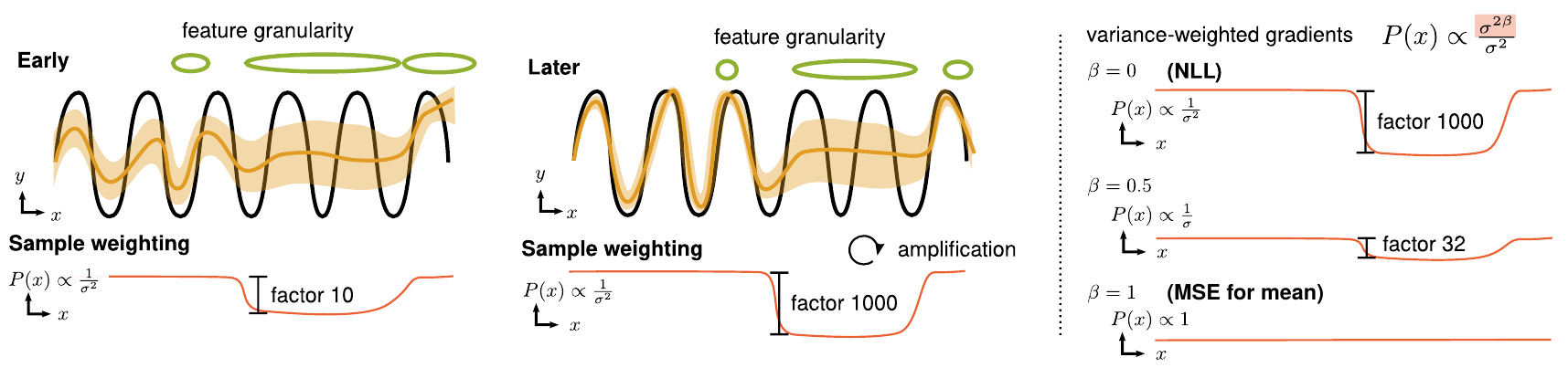
Illustration of an optimization pitfall when training probabilistic neural networks to predict aleatoric uncertainties with NLL (negative log-likelihood) and our solution. An initial inhomogeneous feature space granularity results early on in different fitting quality. The implicit weighting of the squared error in NLL can be seen as a biased data-sampling. Badly fit parts are increasingly ignored during training. On the right, the effect of our solution on the relative importance of data points is shown.
In this project, we investigate learning probabilistic neural networks, that is, neural networks that output an uncertainty-aware prediction. Specifically, we are interested in modeling aleatoric uncertainty, which is the uncertainty inherent in the data. Recognizing such uncertainties is for example useful in model-based RL or for controlled exploration.
The standard approach to modeling (heteroscedastic) aleatoric uncertainty is to predict mean and variance of a Gaussian distribution, and train the model by minimizing the negative log likelihood (NLL) of the data. In practice, this approach encounters certain optimization difficulties which lead to suboptimal predictive accuracy. In this project, we investigated the reasons behind this phenomenon and found that it is related to unequally weighted gradients across the data. We identify a simple solution, which call beta-NLL, that simply reweights the gradients in the loss. We show that the new loss leads to higher accuracy, calibrated uncertainties, is robust to hyperparameters and simple to implement.
A Pytorch implementation of the loss function:
"""Compute beta-NLL loss
:param mean: Predicted mean of shape B x D
:param variance: Predicted variance of shape B x D
:param target: Target of shape B x D
:param beta: Parameter from range [0, 1] controlling relative
weighting between data points, where `0` corresponds to
high weight on low error points and `1` to an equal weighting.
:returns: Loss per batch element of shape B
"""
loss = 0.5 * ((target - mean) ** 2 / variance + variance.log())
loss = loss * (variance.detach() ** beta)
