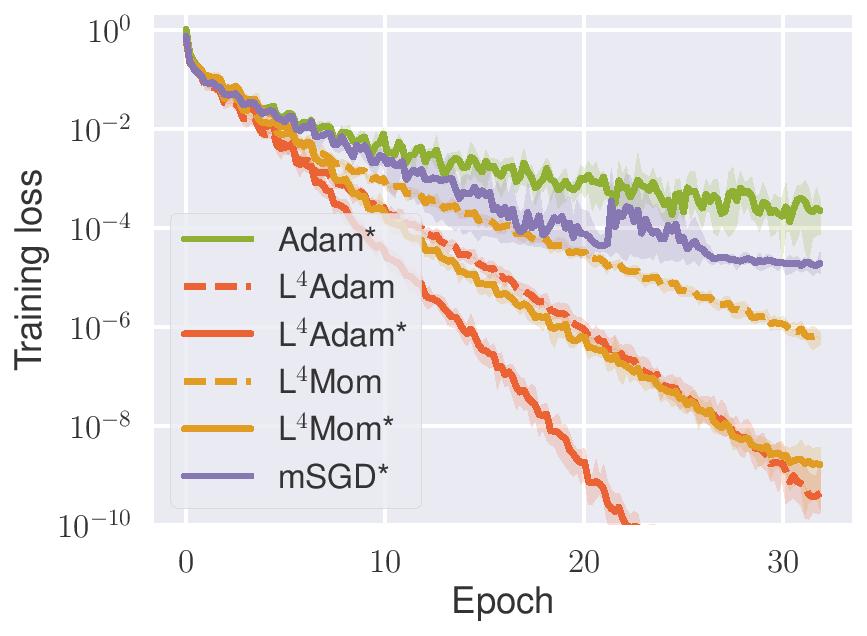
Training progress of multilayer neural networks on MNIST. Average (in log-space) training loss with respect to five restarts with a shaded area between minimum and maximum loss (after log-space smoothing).
Stochastic gradient methods are the driving force behind the recent boom of deep learning. As a result, the demand for practical efficiency as well as for theoretical understanding has never been stronger. Naturally, this has inspired a lot of research and has given rise to new and currently very popular optimization methods such as Adam, AdaGrad, or RMSProp, which serve as competitive alternatives to classical stochastic gradient descent (SGD).
However, the current situation still causes huge overhead in implementations. In order to extract the best performance, one is expected to choose the right optimizer, finely tune its hyperparameters (sometimes multiple), often also to handcraft a specific stepsize adaptation scheme, and finally combine this with a suitable regularization strategy. All of this, mostly based on intuition and experience.
We propose [ ] a stepsize adaptation scheme for stochastic gradient descent.
It operates directly with the loss function and rescales the gradient in order to make fixed predicted progress on the loss.
We demonstrate its capabilities by conclusively improving the performance of Adam and momentum optimizers.
The enhanced optimizers with default hyperparameters
consistently outperform their constant stepsize counterparts, even the best ones,
without a measurable increase in computational cost.
The performance is validated on multiple architectures including dense nets, CNNs, ResNets, and the recurrent Differential Neural Computer on classical datasets MNIST, fashion MNIST, CIFAR10 and others. The results are presented at the Neural Information Processing Systems (NeurIPS) 2018. The code is available at github/martius-lab repository.
