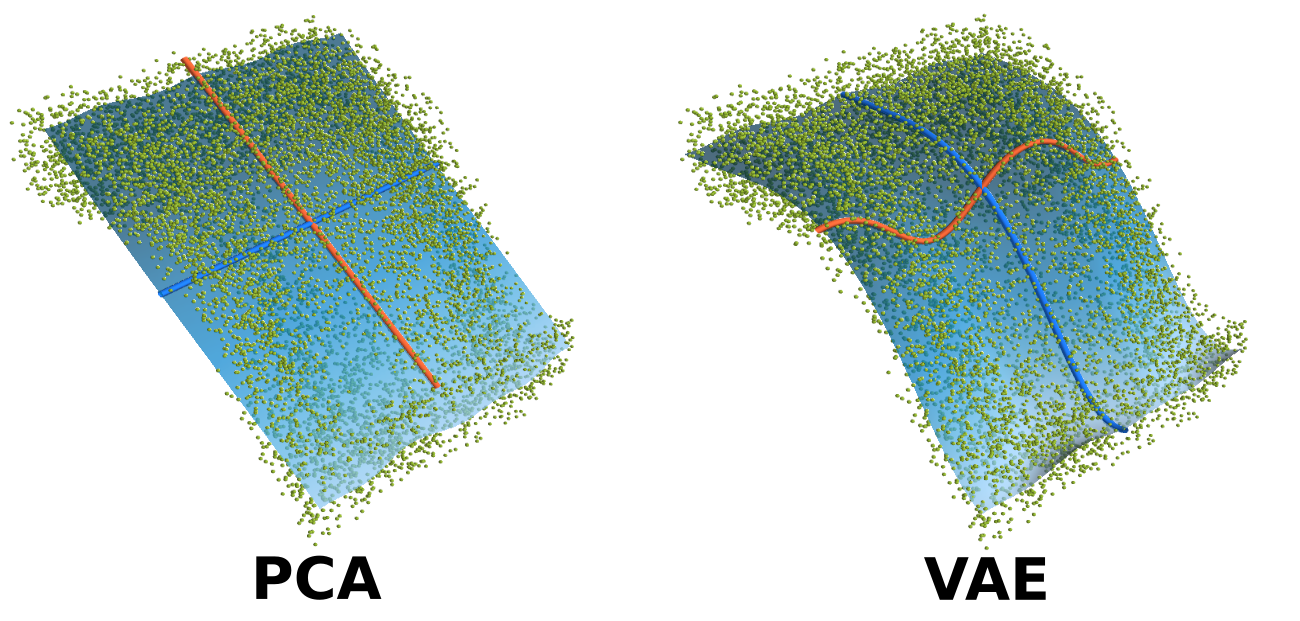
A comparison of the Eigenbasis retrieved through PCA and a non-linear VAE architecture on a synthetic task.
Learning meaningful, low-dimensional representations of data is a challenging problem. Particularly for an autonomously learning system, representations learned from observations can play a crucial role. Consider for example a system that receives many images of faces and is capable of finding out that there are common factors explaining most of the visible characteristics, such as gender, or hair color. Variational Autoencoders (VAEs) can do this to an astonishing extent, but it was unclear why VAEs actually have this ability. We found that the reason is a byproduct of simplifying the learning objective to make the method tractable and suitable for applications [ ]. Interestingly, this insight allowed us to connect VAEs to the classical method of principle component analysis. Furthermore, we then used this understanding to demonstrate that VAEs solely rely on the consistency of local structures in the datasets. In particular, we show that adding small elaborate perturbations to existing datasets prevent the VAE on picking up such convenient structures, yielding new insights into which types of inductive biases and weak supervisions can reliably improve the quality of learned representations [ ]. In the future, we hope to utilize this knowledge for further advances in general data analysis.
